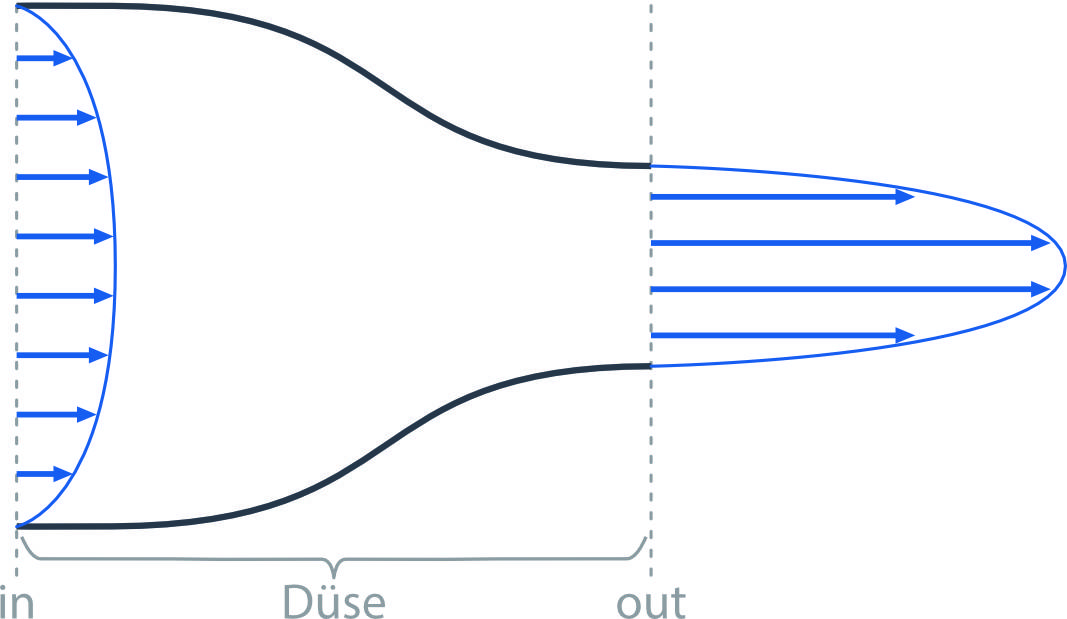
The goal shall be to characterize the current through the nozzle based on the variables pressure p, mass flow rate \(\mathsf{\dot{m}}\) and cross-sectional area A. Using two of the conservation equations of fluid mechanics:
- the conservation of mass, and
- the conservation of energy
between two point of the current, the inlet (in) and outlet (out)) of the nozzle, leads to the following formulas:
\( \begin{align} \mathsf{ \varrho_{in} \cdot A_{in} \cdot u_{in} } & = \mathsf{ \varrho_{out} \cdot A_{out} \cdot u_{out} = \dot{m}} \tag{1} \\ \mathsf{ p_{in} + \frac{1}{2} \varrho_{in} \cdot u_{in}^2 + \varrho_{in} \cdot g \cdot h } & = \mathsf{ p_{out} + \frac{1}{2} \varrho_{out} \cdot u_{out}^2 + \varrho_{out}\cdot g \cdot h + \Delta p_v }\tag{2} \end{align}\)
Formula (1) states that the mass flow rate \(\mathsf{\dot{m}}\) remains constant downstream. Formula (2) is known as Bernoulli’s principle and describes the conversion of mechanical energy resulting from pressure, kinetic energy and potential energy along the filament of flow. Occurring energy loss dissipates into thermal energy and is represented in the factor \(\mathsf{\Delta p_v}\). Other unknown variables in formulas (1) and (2) are the mass density \(\mathsf{\varrho}\), the velocity \(\mathsf{u}\) and the geodetic height \(\mathsf{h}\). The gravitational acceleration \(\mathsf{g}\) shall be approximated through through \(\mathsf{g\approx 9,81 \frac{m}{s^2}}\).
Both Formulas already include simplifications applied to the Navier-Stokes equations. The Navier-Stokes equations are capable of describing these current behaviors including turbulent phenomena completely, however it can only be solved with numerical approximations due to its complexity. Therefore, Bernoulli’s principle shall hence be used and further simplified:
- due to only small changes in the geodetic height potential energy will be disregarded
- the conversion of mechanical energy resulting from pressure into kinetic energy shall be without loss (\(\mathsf{\Delta p_v=0}\))
- the fluid shall be incompressible, e.q. water (\(\mathsf{\varrho_{in} = \varrho_{out} }\))
- pressure differences over the nozzle shall be summarized in \(\mathsf{\Delta p}\) (in general the pressure at the outlet is equal to the ambient pressure
- the average velocity at the outlet is a great deal larger than the one at the inlet (\(\mathsf{u_{out} – u_{in} \approx u_{out} }\))
With the assumptions above the formulas can be simplified:
\( \begin{align} \mathsf{ \dot{m} } & = \mathsf{ \varrho \cdot A_{out} \cdot u_{out} } \tag{1} \\ \mathsf{ \Delta p } & = \mathsf{ \frac{1}{2} \varrho \cdot u_{out}^2 }\tag{2} \end{align}\)
Combining both formulas results in the following:
\( \begin{align} \mathsf{ \dot{m}} &= \mathsf{A_{out} \cdot \sqrt{2 \varrho \cdot \Delta p } } \end{align} \)
This formula provides us with a simple interrelation of material throughput, loss of pressure and cross-sectional area of the current. It also provides the formula for the nozzle capacity C. A comparison with measured data shows a very good agreement. We can hence devise the following relations between the variables:
- A linear relation connects the material throughput to the cross-sectional area, i.e. a doubling of the cross-sectional area will result in a doubling of the material throughput regarding a constant pressure.
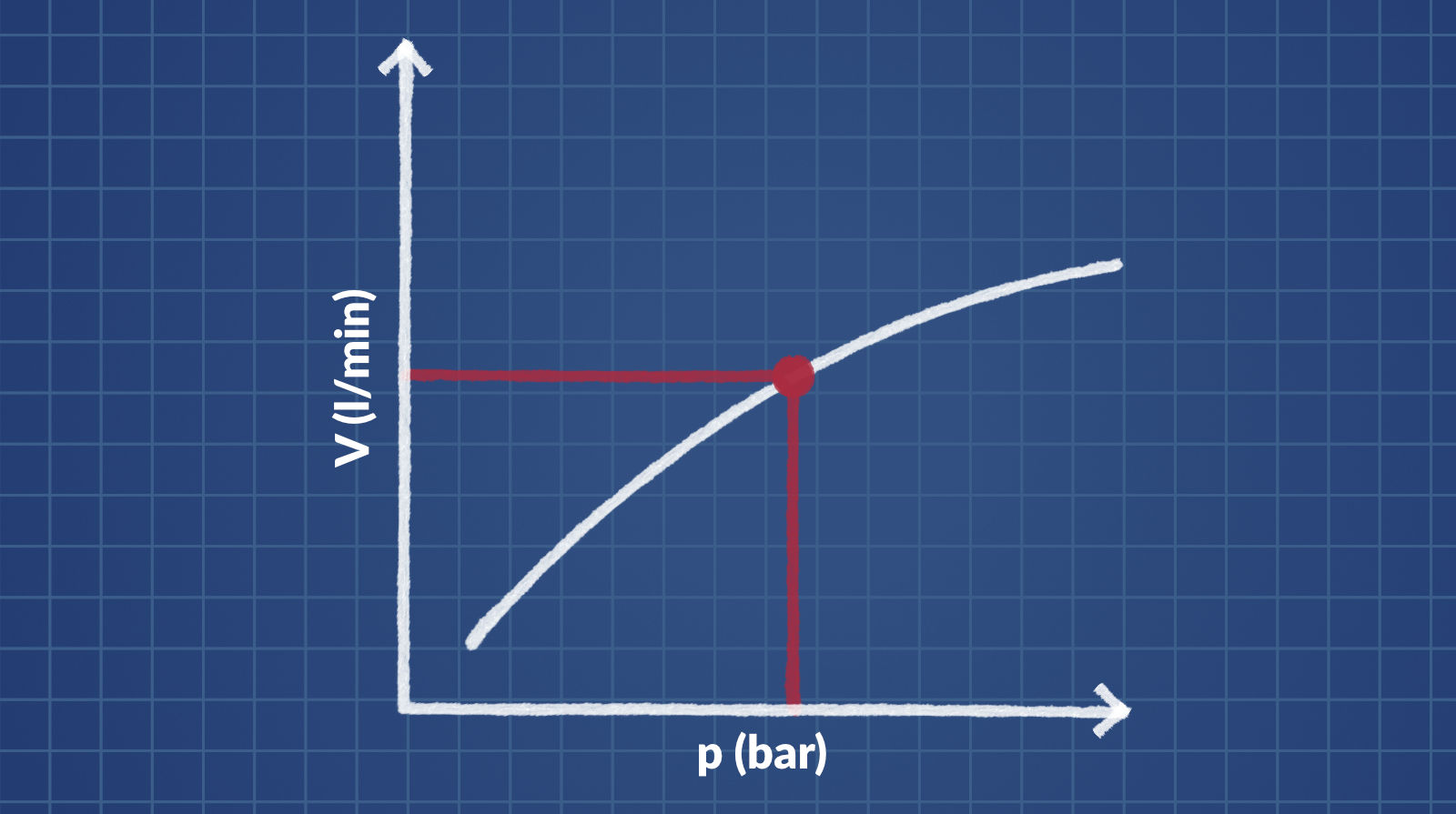
- The volumetric flow rate is connected to the pressure by a root relation. A quadruplication of the pressure will lead to a doubling in flow capacity.