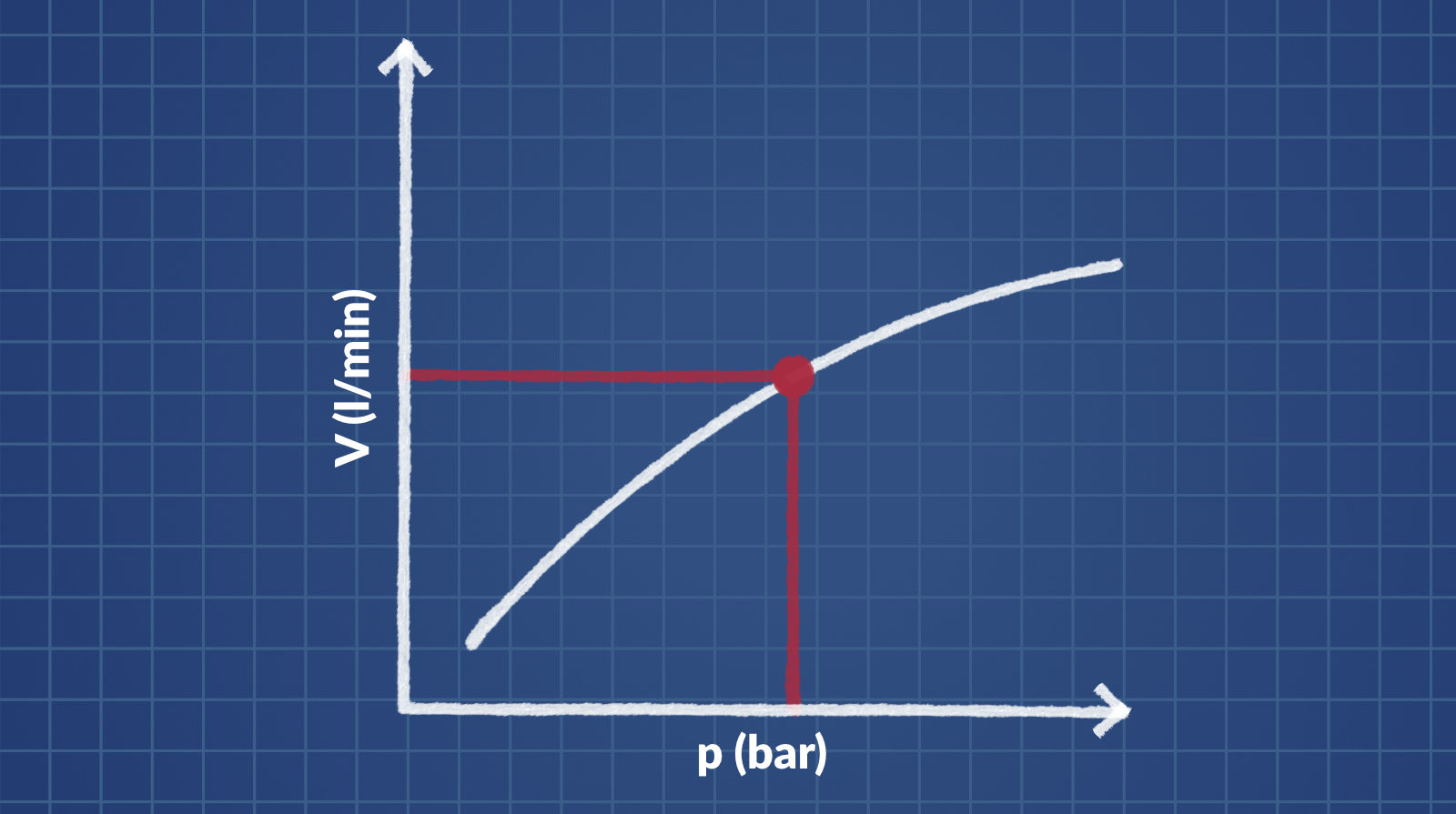
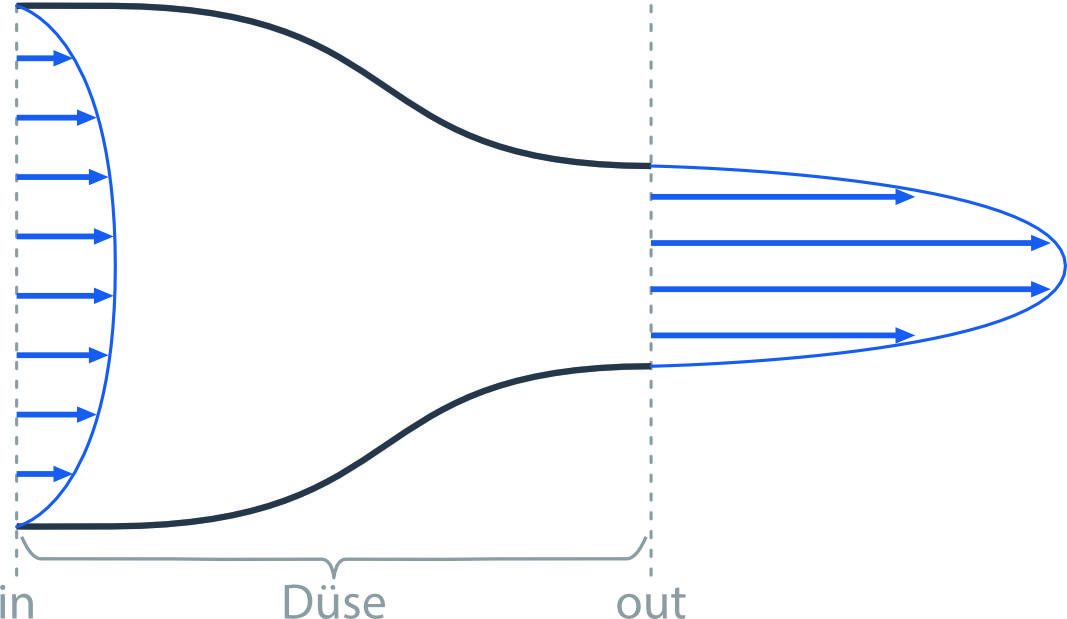
Es gibt Düsen in verschiedenen Formen und Größen. Ein wichtiger Kennwert für die Auswahl der passenden Düse ist die Düsengröße. Tendenziell hat eine große Düse bei gleichem Druck einen höheren Durchsatz am flüssigen oder gasförmigen Arbeitsmedium als eine kleine Düse. Aber auch die Form der Düse hat einen Einfluss darauf wie viel bei einem bestimmten Druck durch die Düse strömt.
Zusätzlich entscheidet die Düsenform grundlegend über das Sprühbild. Die nebenstehende Abbildung zeigt einige Düsenformen am Beispiel einer Reinigungsbrause. Eine Lochdüse produziert z. B. einen Vollstrahl, eine Schlitzöffnung wird häufig für Flachstrahldüsen verwendet und eine Hohlkegeldüse weist typischerweise einen Kegel mit der Spitze in Richtung der Anströmung auf. Die besondere Geometrie von OsciJet Düsen erzeugt einen oszillierenden oder pulsierenden Strahl.
Um trotz der verschiedenen Formen eine gut vergleichbare Kenngröße zu bilden, bezieht sich die Düsengröße nicht etwa auf geometrische Maße der Düse, sondern ist als ein Durchfluss bei einem bestimmten Referenzdruck definiert.
Im Produktsortiment von FDX verwenden wir eine sehr gebräuchliche Definition: